My research interests are in structure-preserving numerical methods, data-driven/machine learning methods, as well as their applications in the mathematical sciences. Currently, I focus on three related areas:
- Structure-Preserving Numerical Methods
- Structure-Preserving Data-Driven/Machine Learning Methods
- Applications of Structure-Preserving Methods
I also belong to a PIMS Collaborative Research Group (2024-2027) on Structure-Preserving Discretizations and their Applications.
Below are some past and on-going projects that I worked on with my collaborators and students.
For more details, see a list of my publications.
Structure-Preserving Numerical Methods
- Minimal l2 Norm Discrete Multiplier Method
with E. Schulz
We introduced Minimal Norm Discrete Multiplier Method (MN-DMM) to extend the practical applicability of the original DMM, leading to a unique consistent globally defined conservative scheme for large dynamical systems with multiple invariants. By preserving all five conserved quantities (energy, angular momentum, speed) for Schwarzschild geometry, MN-DMM can compute accurate geodesics at larger time steps than traditional nonconservative integrators.
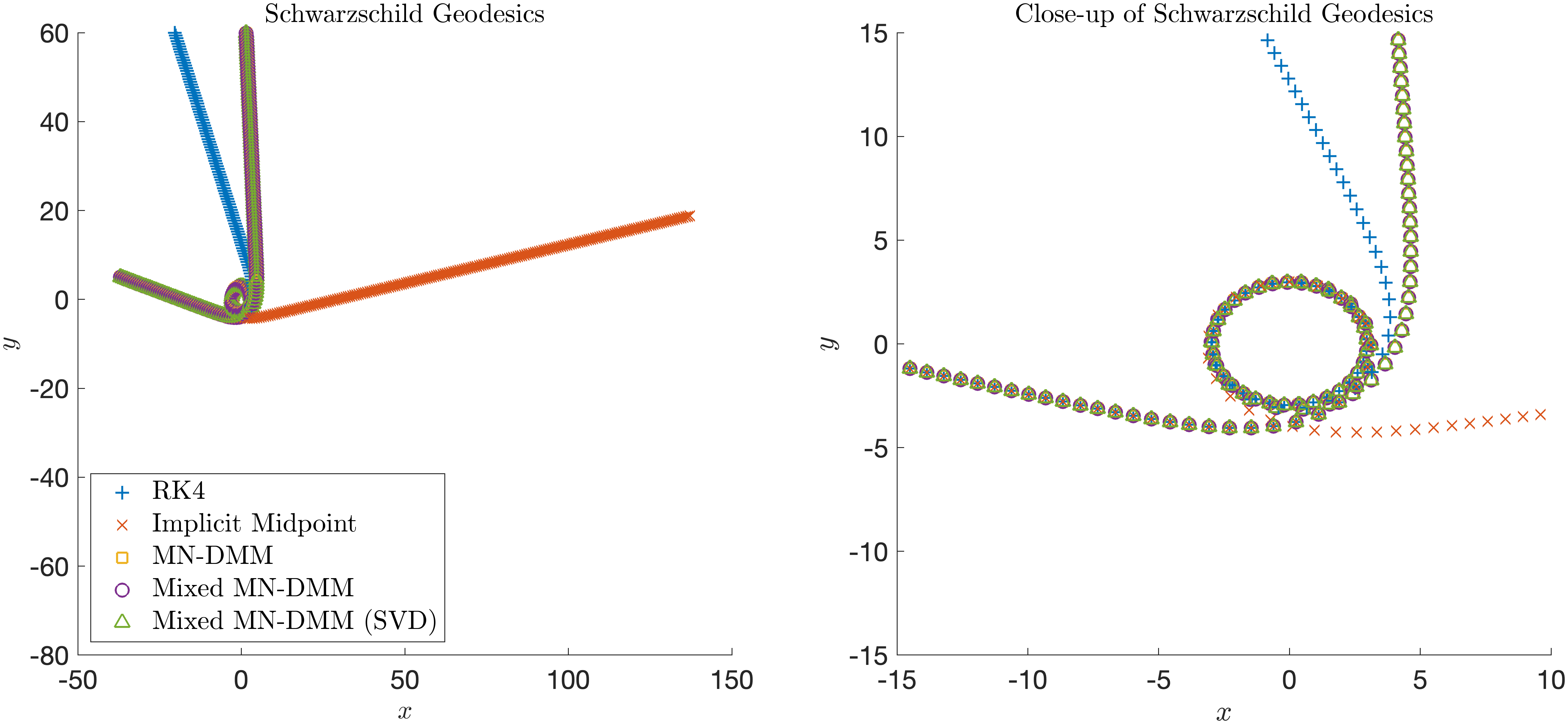
- On the Arbitrarily Long-term Stability of Conservative Methods
with J.-C. Nave
Symplectic methods possess favourable long-term properties, such as near conservation of energy over exponentially long time and at most linear growth in global error for completely integrable systems. In this work, we showed that under appropriate conditions, the global error of conservative methods is bounded for an arbitrarily long time.
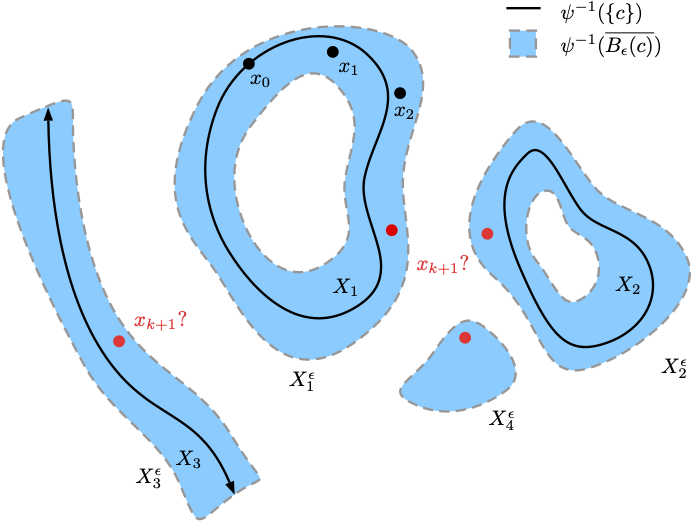
- Conservative Methods for Dynamical Systems
with A. Bihlo and J.-C. Nave
We introduced the Discrete Multiplier Method as a novel systematic approach to construct conservative finite difference schemes for quasilinear first-order ODEs with multiple conserved quantities of arbitrary forms. We derived discrete conditions for consistent conservative schemes of arbitrary order and devised various novel conservative schemes, including Hamiltonian systems, Poisson systems and dissipative systems.
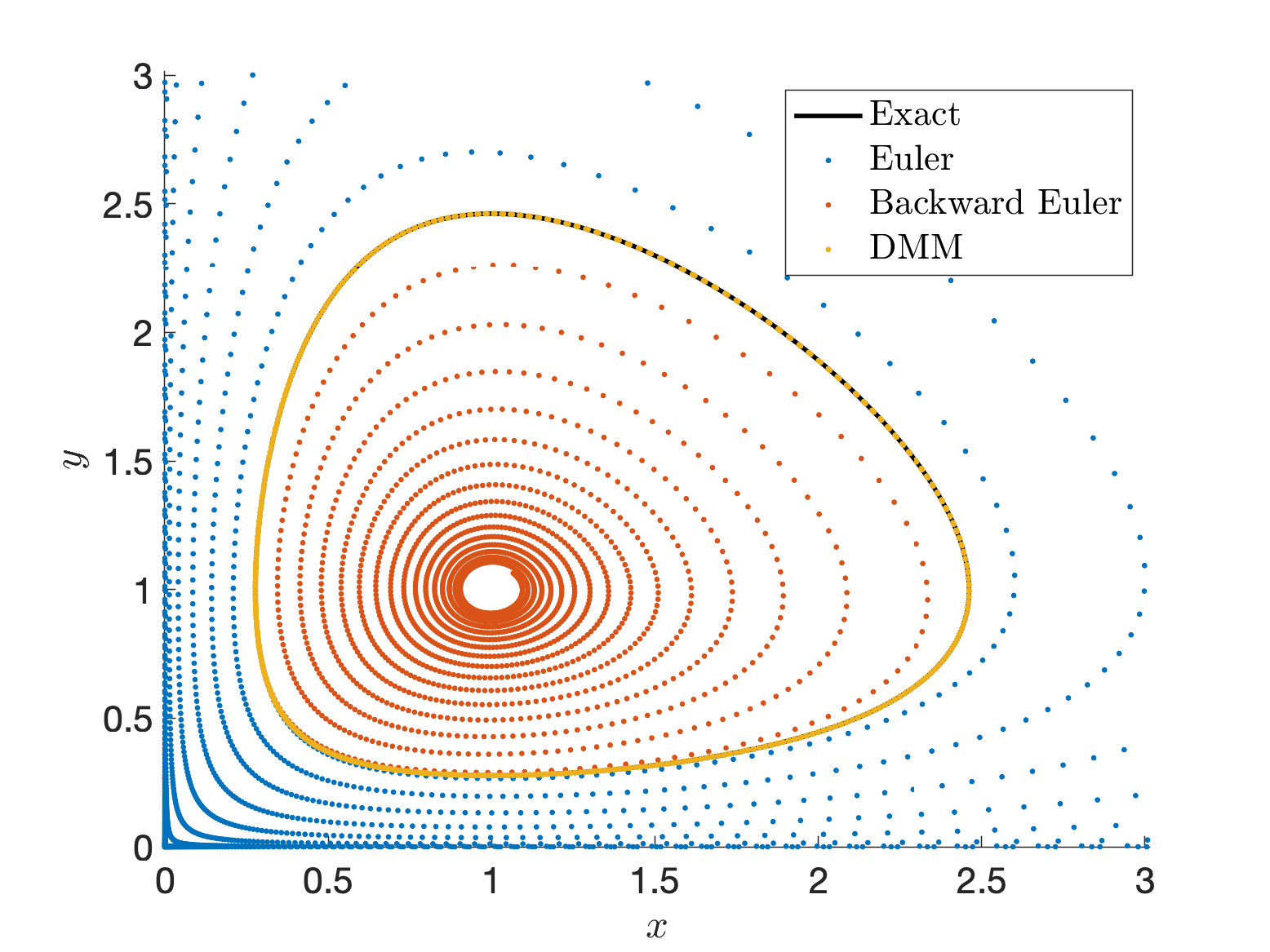
Structure-Preserving Data-Driven/Machine Learning Methods
-
Conservative Hamiltonian Monte Carlo
with G. McGregor
Hamiltonian Monte Carlo (HMC) is a Markov Chain Monte Carlo algorithm often used to sample posterior distributions for Bayesian statistics. To generate new proposals, symplectic integrators are typically used to solve a Hamiltonian system associated with the posterior distribution, which can have low acceptance probability on large dimensional problems. Instead, we propose the use of conservative integrators which preserve the energy up to machine precision to improve the sampling efficacy of HMC.
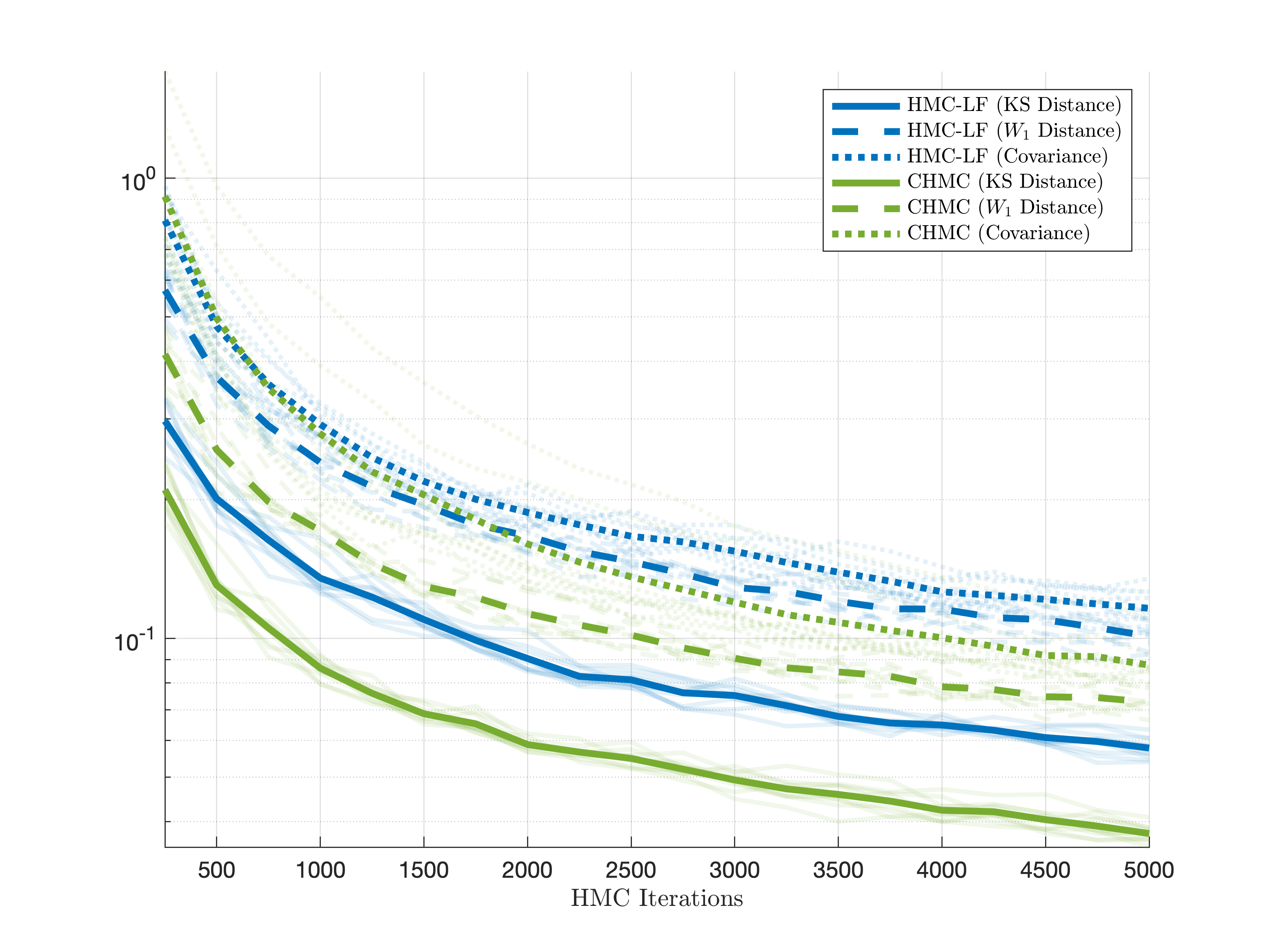
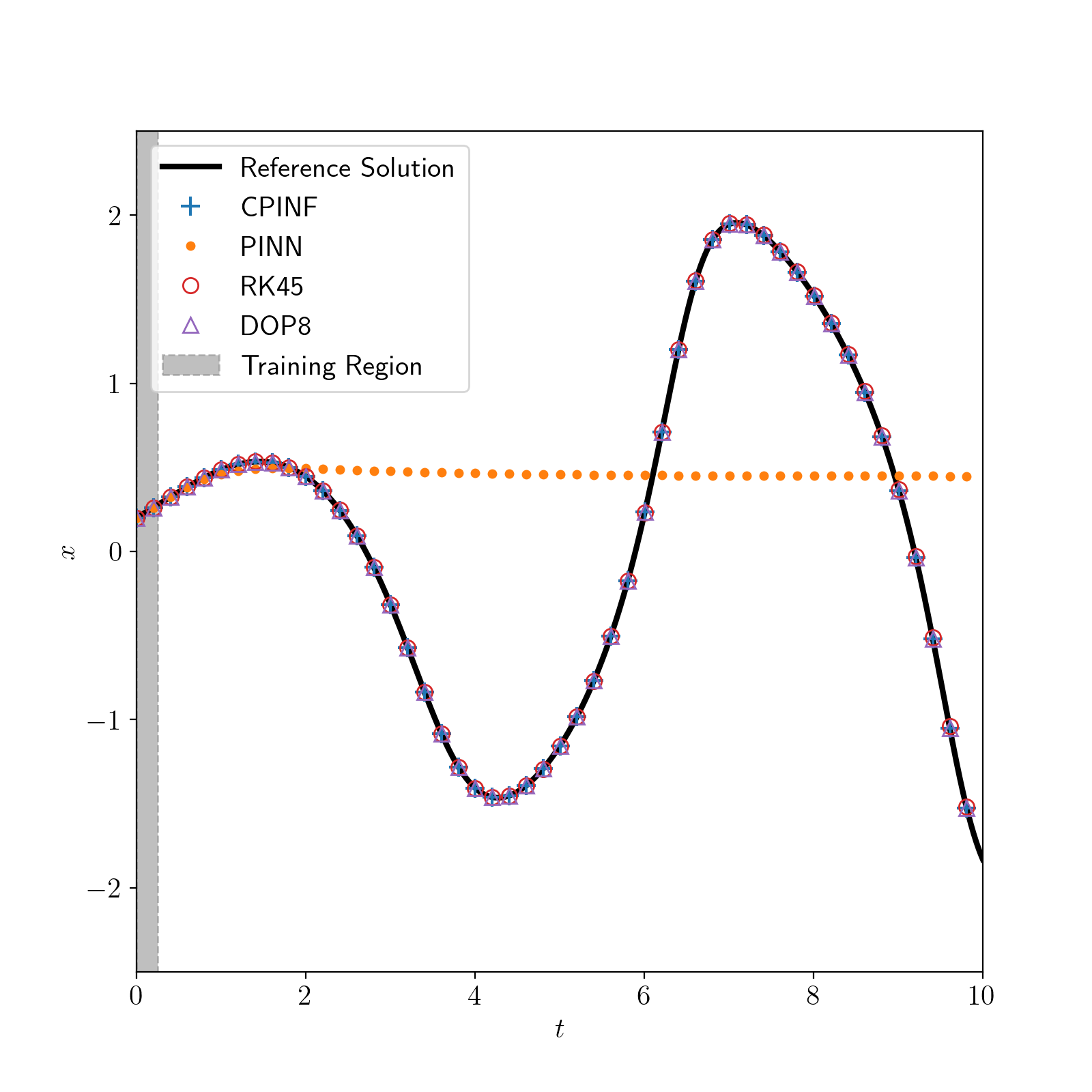
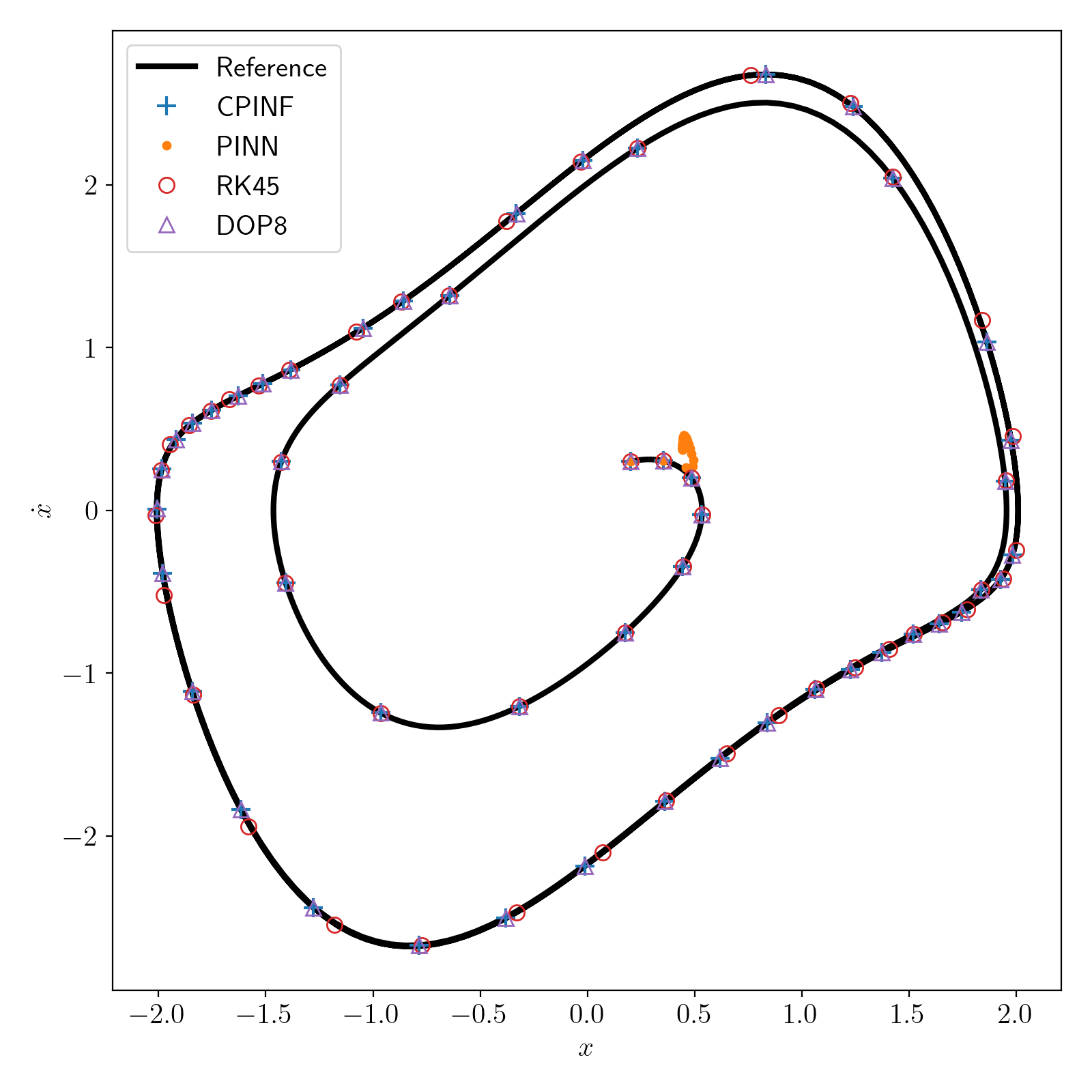
- Compositional Physics-Informed Neural Flow
with P. Lalwani
We extend Physics-Informed Neural Network (PINN) to incorporate the compositional nature of flow maps. Under appropriate conditions, we showed that its error can be bounded above a posteriori by the empirical loss and quadrature/sampling error of the true loss.
Applications of Structure-Preserving Methods
- Fully Discrete Entropy-Dissipative and Conservative Particle Methods for the Aggregation-Diffusion and Landau Equations
with J. Hu and S. Q. Van Fleet
Many kinetic equations possess conserved quantities (mass, momentum, energy) and dissipative quantities (entropy, fisher information). For a class of regularized particle methods for nonlocal diffusion equations and the Landau equation, we showed that discrete gradient integrators can be applied to preserve their conserved and dissipative quantities.

- Conservative Integrators for Many-Body Problems
with A. Bihlo and J.-C. Nave
Using DMM, we showed conservative methods can be derived for many-body problems with multiple conserved quantities. In particular, we derive novel conservative second-order schemes for many-body problems, including n-species Lotka-Volterra system, n-body problem with radially symmetric potential, n-point vortex model in the plane and on the unit sphere.

