The Noise-Collector

The ability to detect sparse signals from noisy, high-dimensional data is a top priority in modern science and engineering. For optimal results, current approaches need to tune parameters that depend on the level of noise, which is often difficult to estimate. We develop a new parameter-free, computationally efficient, ℓ1-norm minimization approach that has a zero false discovery rate (no false positives) with high probability for any level of noise while it detects the exact location of sparse signals when the noise is not too large.

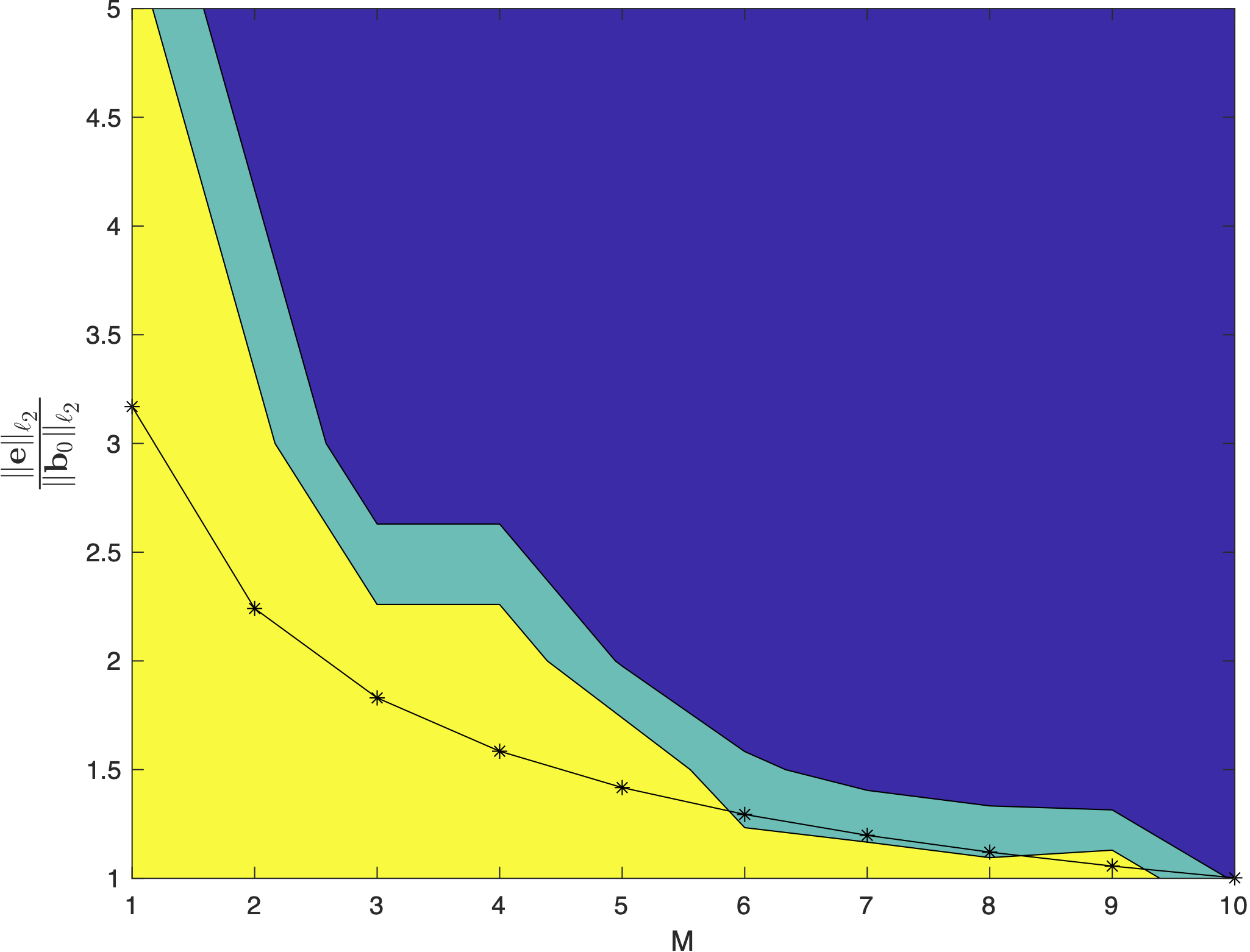
Algorithm performance for exact support recovery. Success corresponds to
the value 1 (yellow) and failure to 0 (blue). The small phase transition zone (green)
contains intermediate values. Ordinate and abscissa are the sparsity (M) and the noise to signal ratio (1/SNR). The black line is the theoretical estimate \(\sqrt{N}/\sqrt{M ln N} \) 

Coherent imaging using phase-less measurements

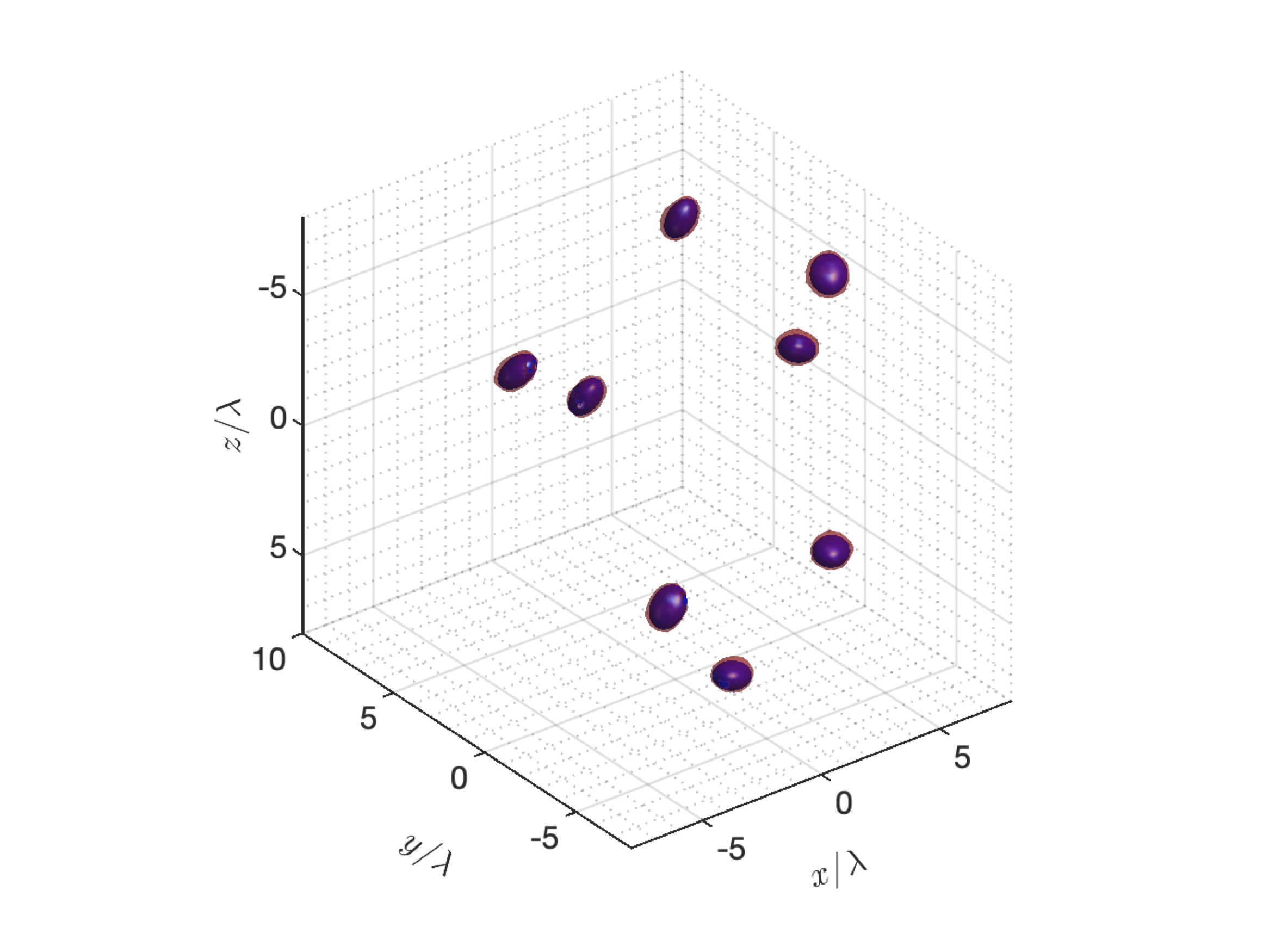
MUSIC image obtained from intensity only measurements

In many applications, especially when using optical or X-ray sources, we can only measure spectral intensities. In order to image coherently in this setup we have to recover the phases of the complex signal. To achieve this, we design appropriate protocols of illuminations which together with the polarization identity are used to recover phase cross-correlations of the imaging system. Our approach guarantees exact recovery of the phase cross-correlations and is efficient for large scale systems. Given the phase cross-correlations, the imaging problem can be successfully solved using an \(\ell_1\) or \(\ell_2\) methodology. There are several challenges that we are addressing: (i) Design appropriate illumination protocols for systems with reduced diversity such as single source/receiver configurations. (ii) Develop statistically stable protocols to mitigate clutter effects.

Satellite imaging through the turbulent atmosphere

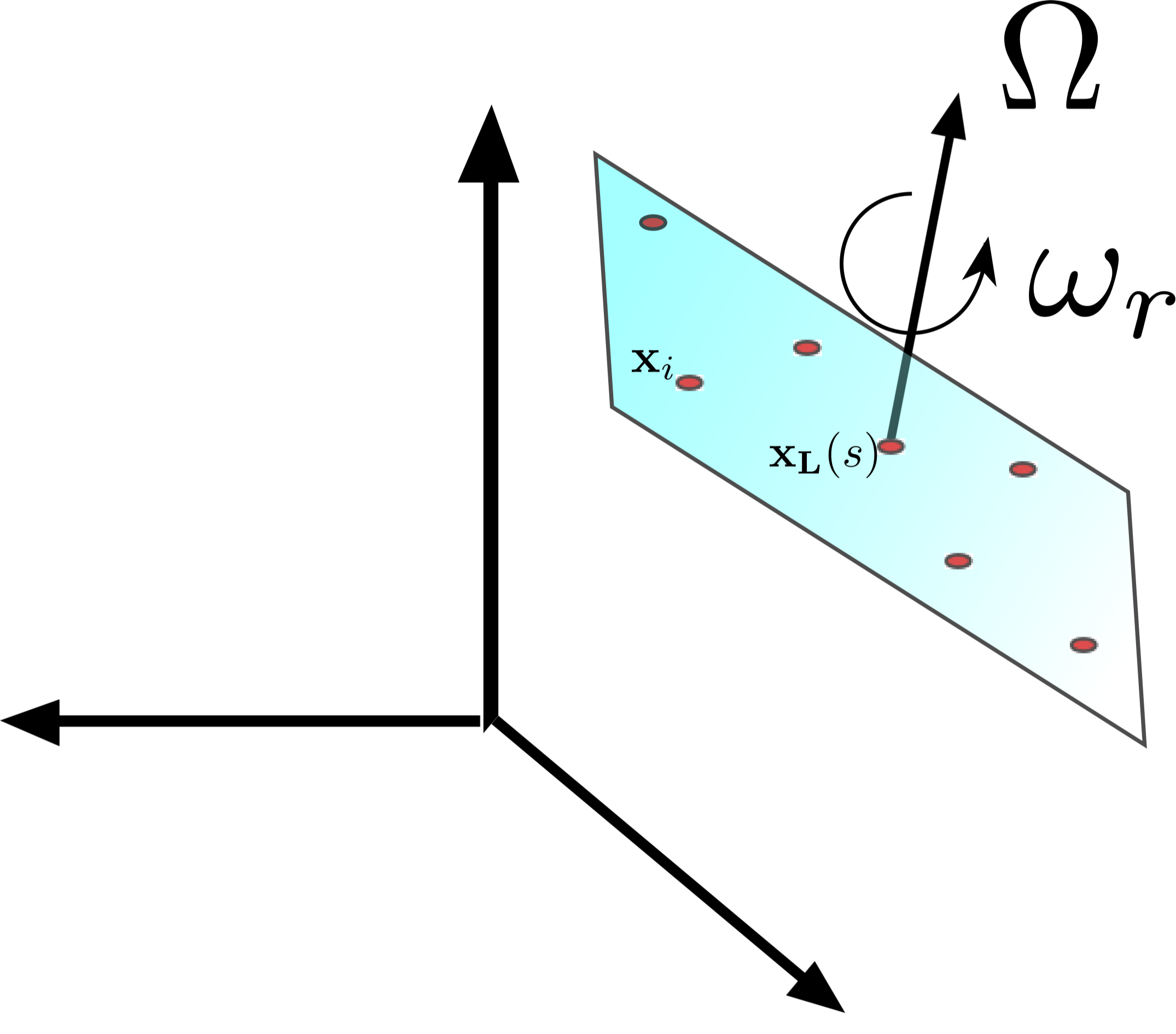
Schematic of rotating satellite

This is a virtual source array imaging problem where the sources are ground-based radar transmitters, while the passive receivers are on airborne platforms flying above the tropopause (at 15km height). The idea is to use cross-correlations of passive recordings in order to image objects (satellites) moving in space. The advantage of this configuration compared to ground-based radar imaging is that by employing the passive array above the complex scattering atmosphere we will minimize the random medium effects on the image. This is an application of correlation based imaging that raises several challenging questions and might lead to new paradigms for satellite imaging. Some of the questions that we are addressing are: What is the resolution and the sensitivity of the imaging function? How do these quantities depend on the number and configuration of platforms? How well do we need to know the source? How do the results compare with the ones of traditional matched field imaging with ground based receivers?