Research

COVID-19 Modeling

In May 2020, we were asked by UC Merced administration, in collaboration with S. Sindi and E. Rutter, to lead modeling efforts of COVID-19 for the UC Merced campus. Since May, we have been working on developing a compartmental differential equation model, conducting simulations, and analyzing results for the spread of COVID-19 on the UC Merced campus. We have been presenting results including infection rates, cumulative infections, and daily incidences as well as looking at testing options for the fall semester. Furthermore, we are analyzing the modification of the infection spread when different interventions are incorporated, including face covering usage, class size caps, and self-isolation of symptomatic people. These results are being used by the UC Merced administration to make decisions related to face to face courses offerings, student housing, quarantine and isolation, and testing and contact tracing.

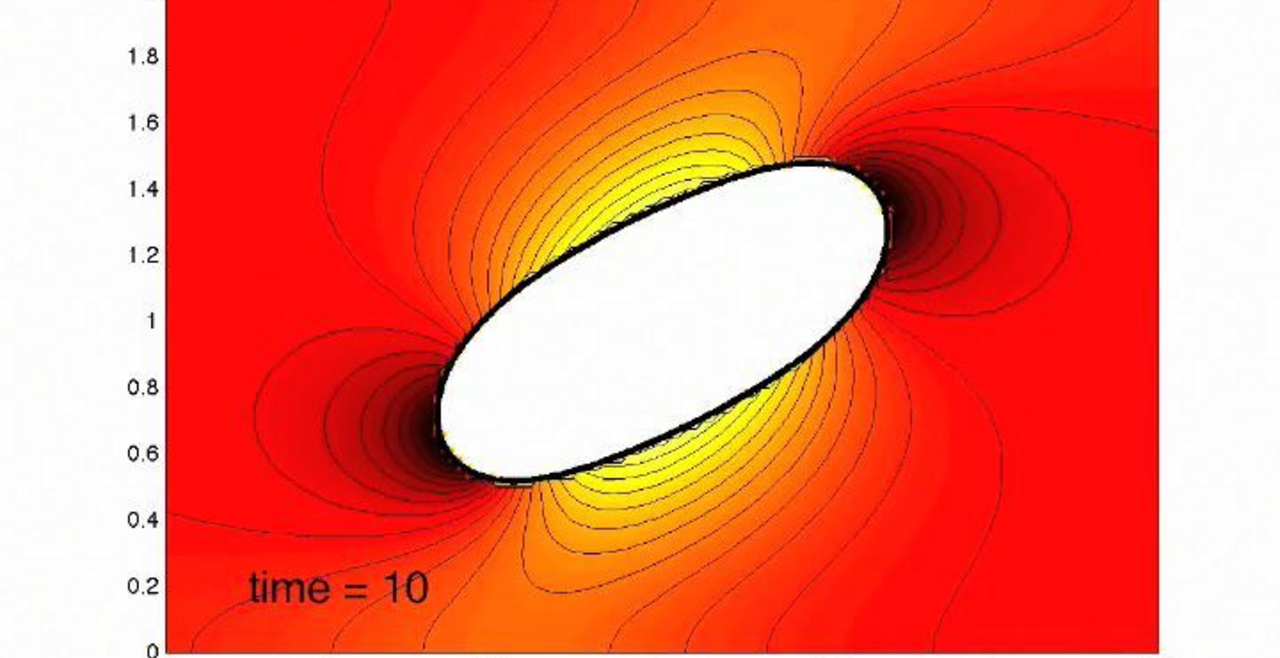
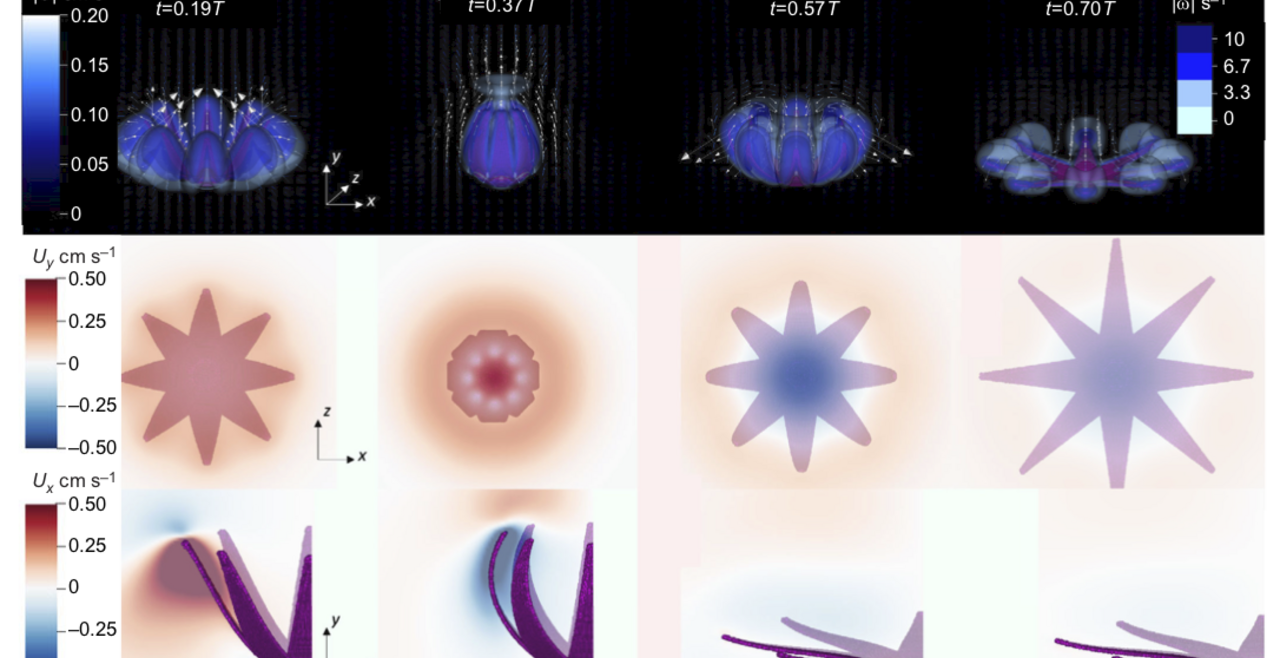
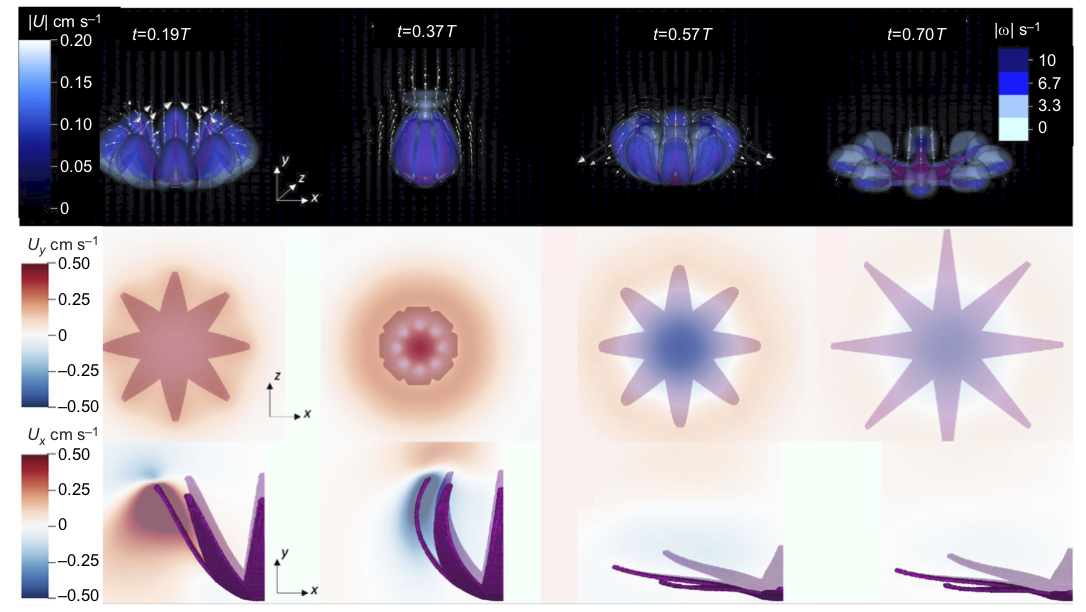
Pulsating Soft Corals

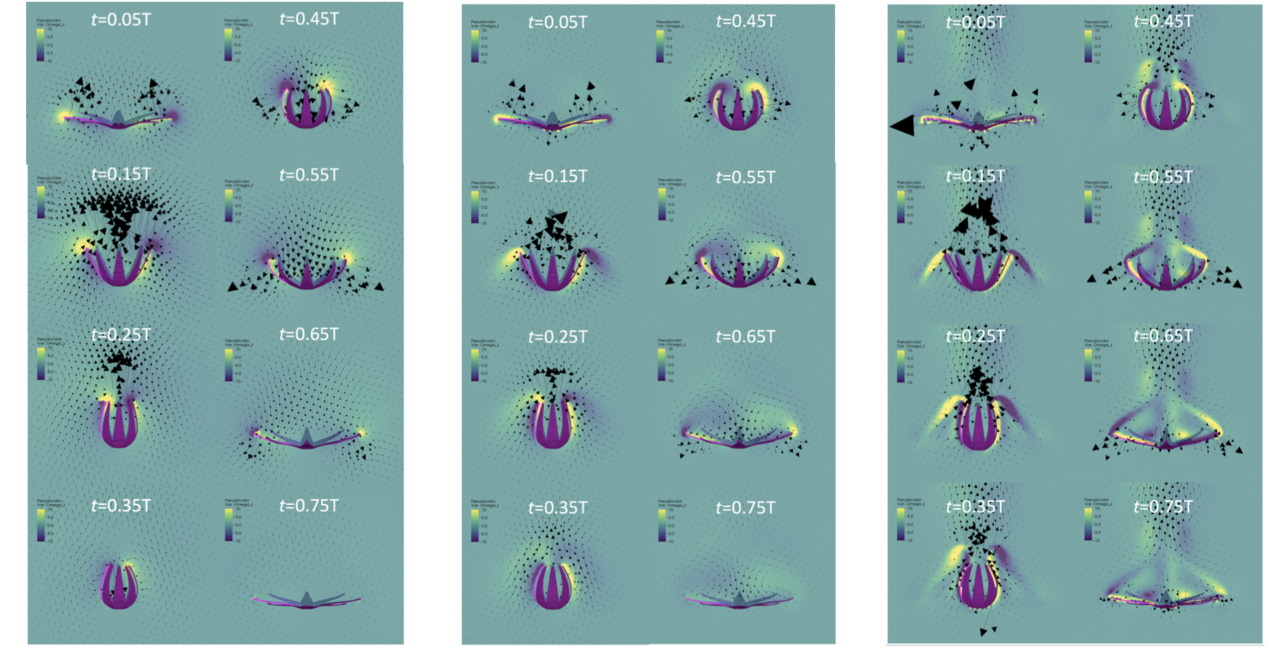
Soft coral of the family Xeniidae have a pulsing motion, a behavior not observed in many other immobile marine organisms. These pulsations consume a large amount of energy, and determining the benefits of this behavior is vital to understanding the evolution of such animals. It is hypothesized that this pulsing allows symbiotic algae to photosynthesize more and provide the corals with significantly greater amounts of carbon. Furthermore, understanding the efficient mixing created by this pulsing motion has many industrial applications. We have been developing and conducting three-dimensional numerical simulations of the pulsations of the coral Heteroxenia fuscescens. These simulations include modeling the resulting fluid flow by solving the Navier-Stokes equations coupled with the immersed boundary method to model coral polyps. We are also developing new mathematical models and numerical methods to couple the coral motion with models of photosynthesis.

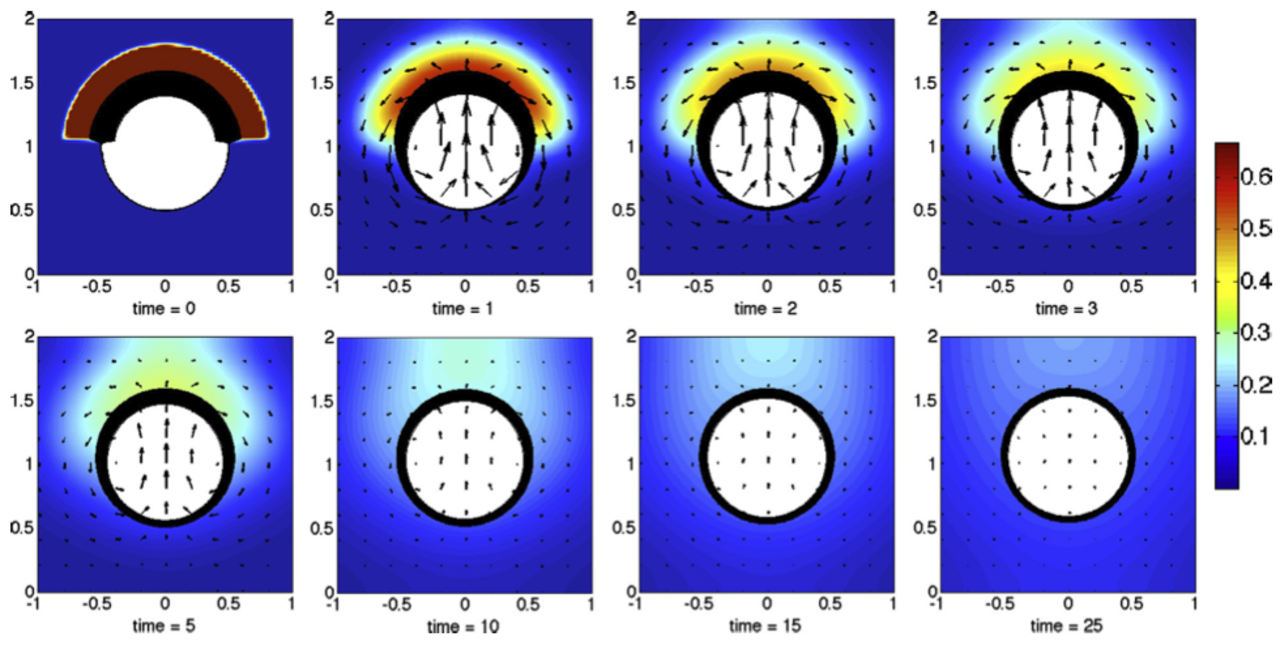
Settling and Rising in Density Stratified Fluids

The effect of density stratification, variations in the density, on marine phenomena is important as these gradients are present in the ocean and atmosphere and play a fundamental role on the observed small-scale fluid dynamics. We have been investigating problems of settling and rising in stratified fluids using a combination of laboratory experiments, modeling, analysis, and numerical simulations.

I. Marine Aggregates

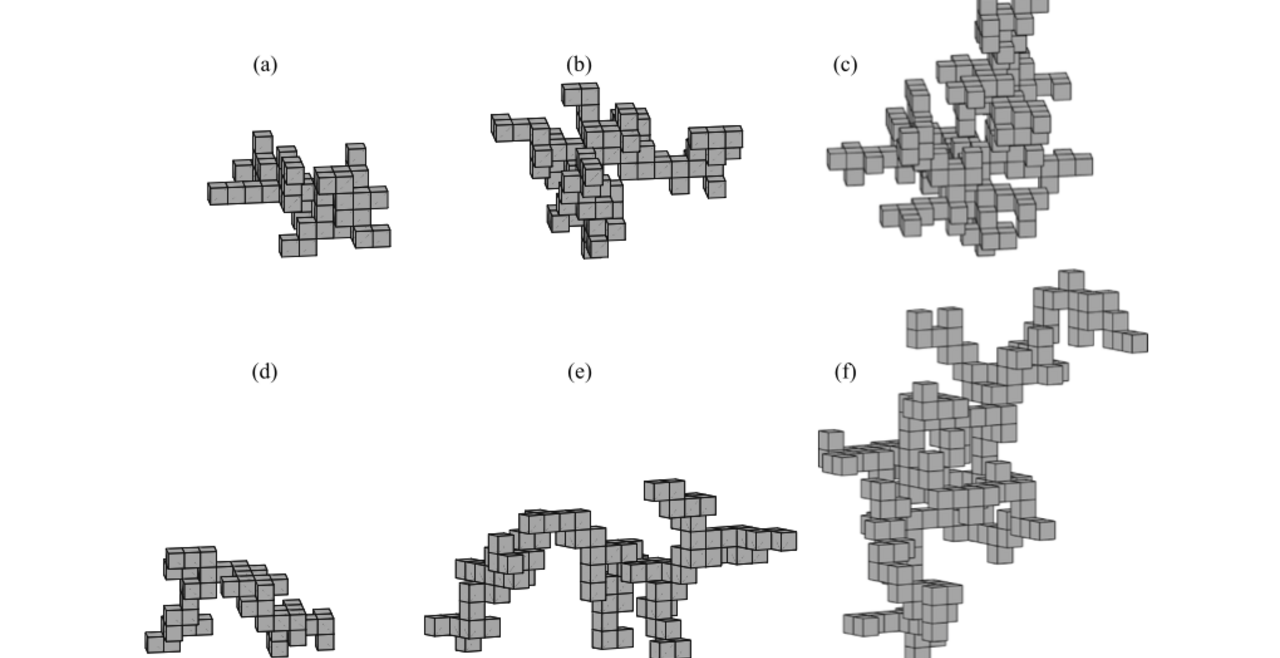
Marine aggregates are porous particles composed of organic and inorganic matter which play a major role in the carbon cycle. These particles form thin layers in the ocean corresponding in location with sharp density gradients, either due to salinity or temperature variations. To understand these dynamics, our focus has been to develop and analytically study a simplified model for a porous sphere settling in stratified fluids, to compare this model with numerical simulations and experiments, and to generalize numerical simulations to more realistic marine aggregates.

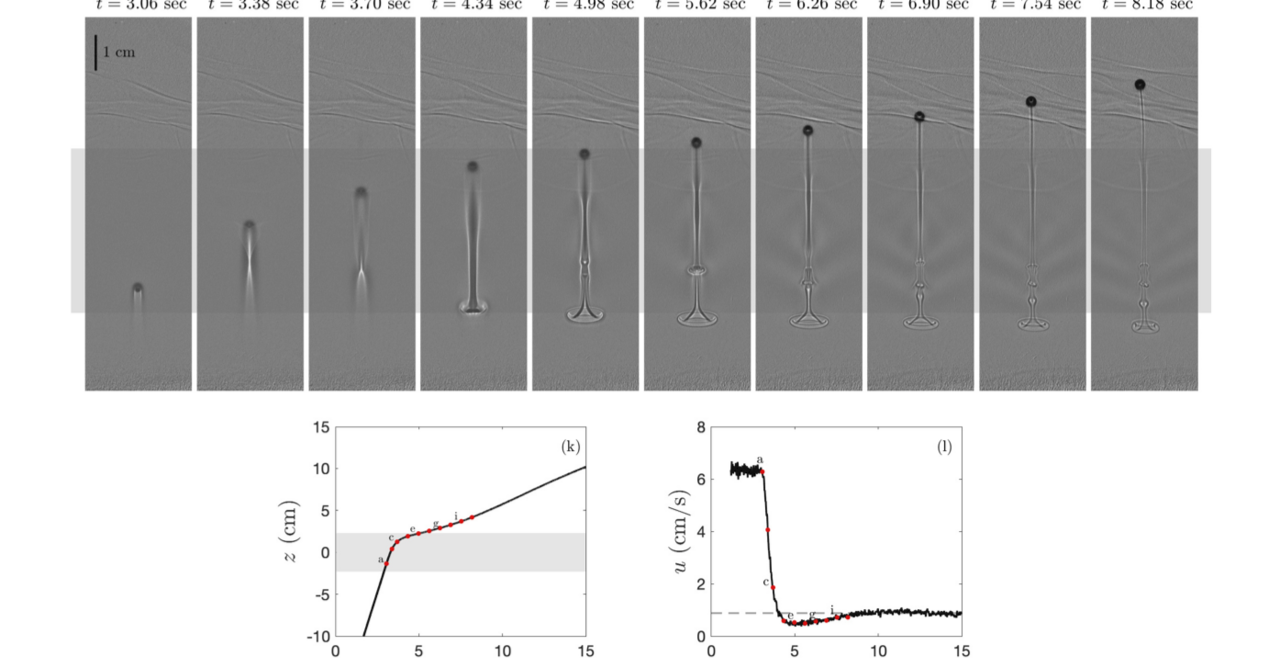
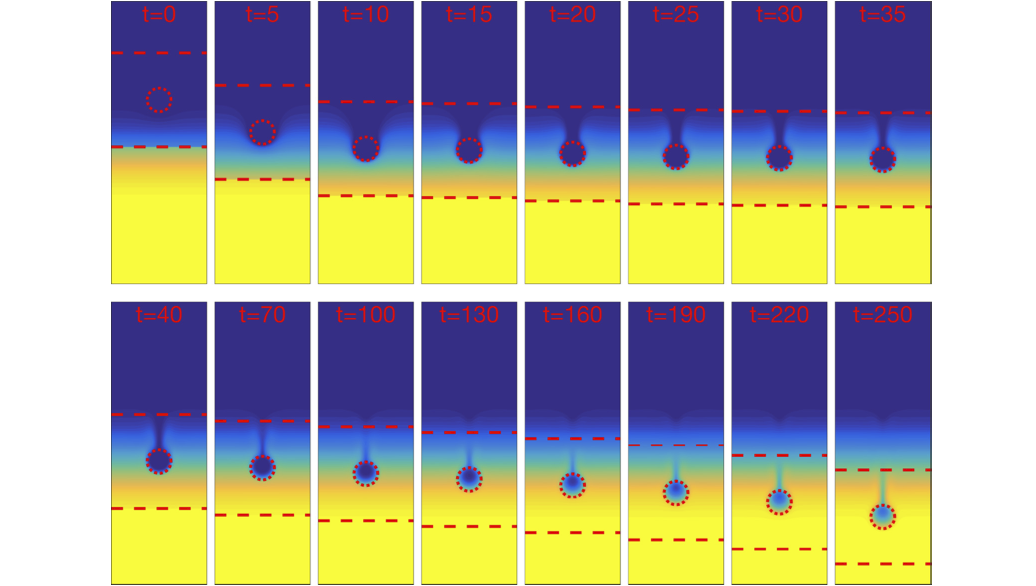
II. Oil Droplets

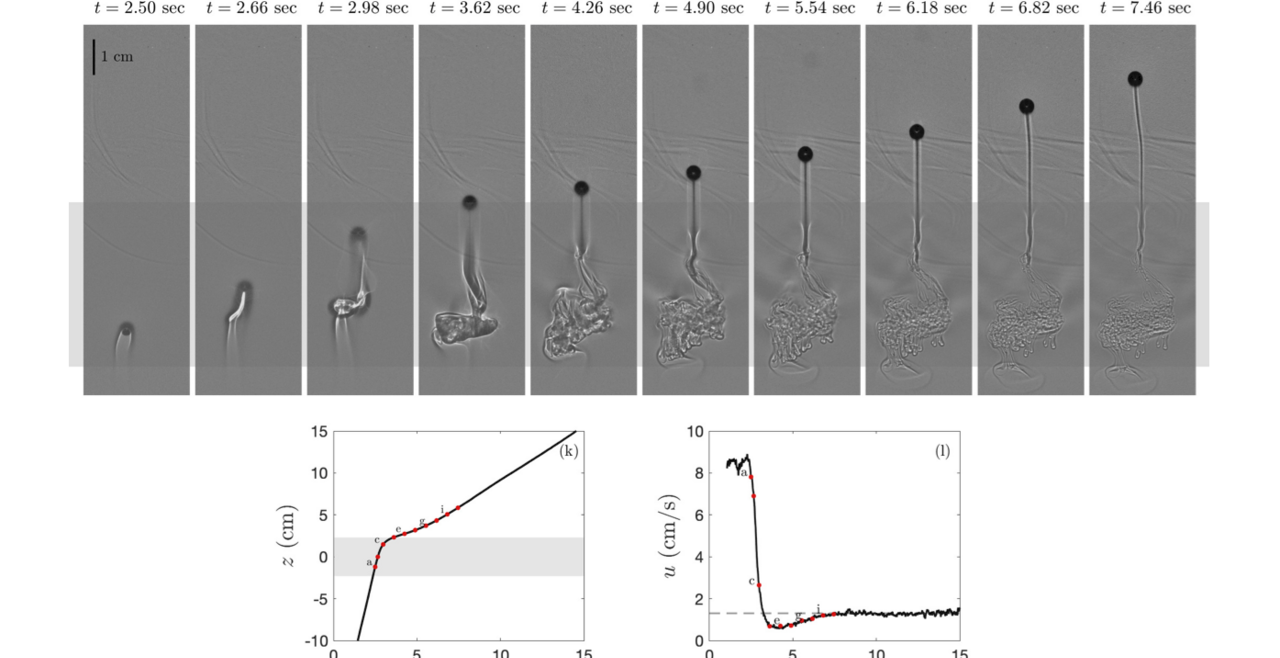
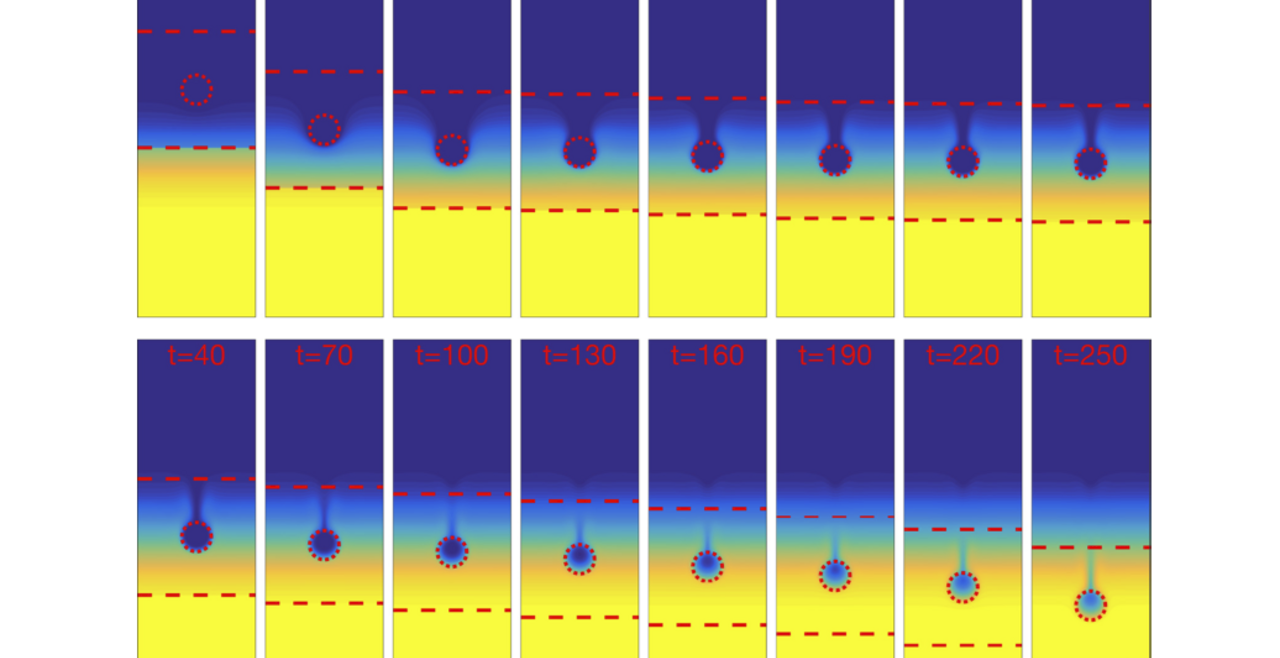
During the Deepwater Horizon oil spill in 2010, millions of barrels of gas and oil were released into the Gulf of Mexico. To be able to quantify the amount of oil released during a spill and to determine the environmental impact of this oil in the ocean we must understand how and why the oil traps below the surface. To gain this understanding, we consider the small-scale fluid dynamics of individual droplets of oil rising in ambient fluid with variations in density. To determine the role of fundamental fluid dynamics on the behavior of droplets rising in stratified fluids, we have developed experiments, mathematical models, and computational tools to make predictions.

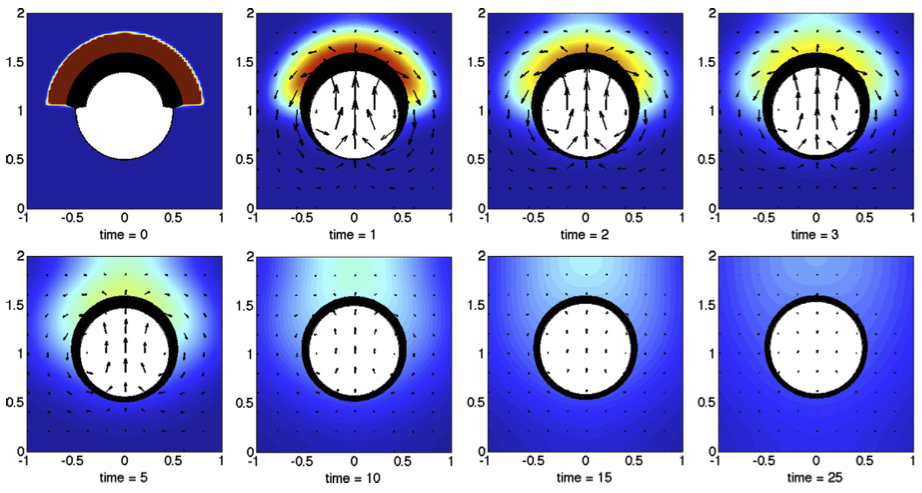
III. Dense-Core Miscible Vortex Rings

The settling of dense miscible vortex rings is an important component of settling and rising phenomena in density stratified fluids. Experimental parameter studies have been conducted of miscible vortex rings settling in sharply stratified ambient fluids. Full three-dimensional variable density Navier-Stokes simulations have been conducted for this problem. We ran simulations for a dense-core vortex ring settling in homogeneous ambient fluids and were able to show good quantitative agreement with experiments, and then in the more complex case of a sharply stratified ambient fluid, good qualitative agreement. In the two-layer case, we were able to simulate a critical phenomenon, trapping at the interface between the two layers or escape through the interface, that we had observed in the experiments.

R. Camassa, S. Khatri, R. McLaughlin, K. Mertens, D. Nenon, C. Smith, and C. Viotti, Numerical simulations and experimental measurements of dense-core vortex rings in a sharply stratified environment, Computational Science & Discovery, 6:014001, 2013 (pdf) (link)

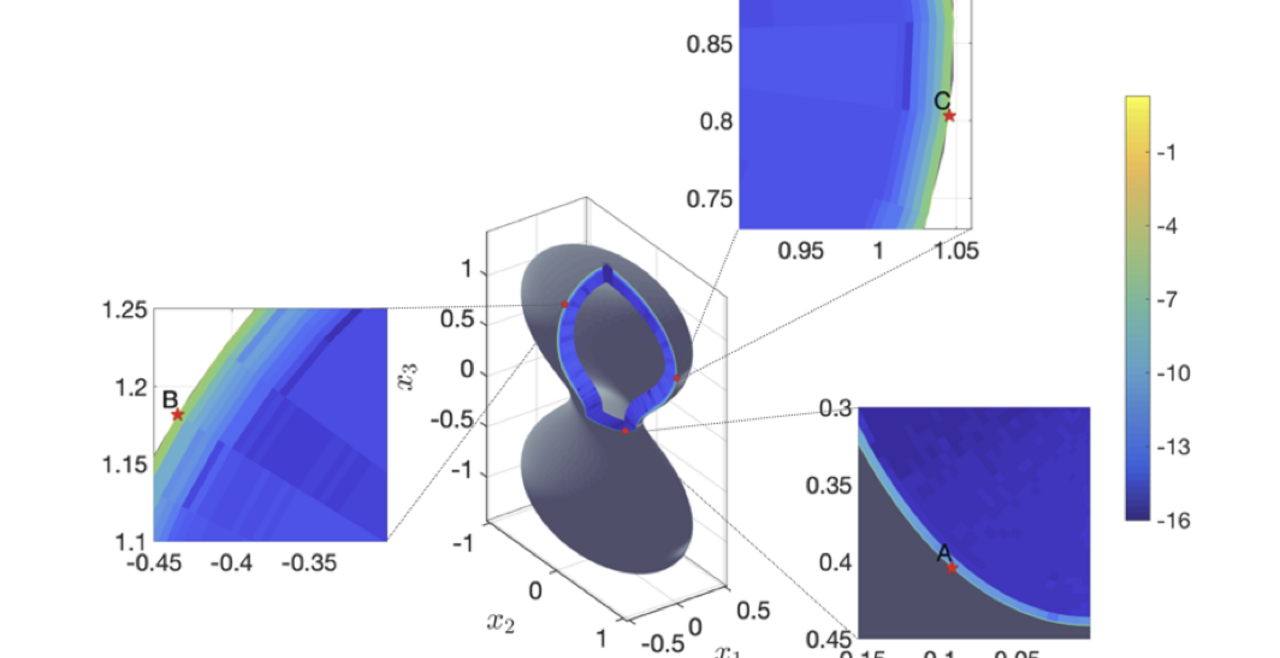
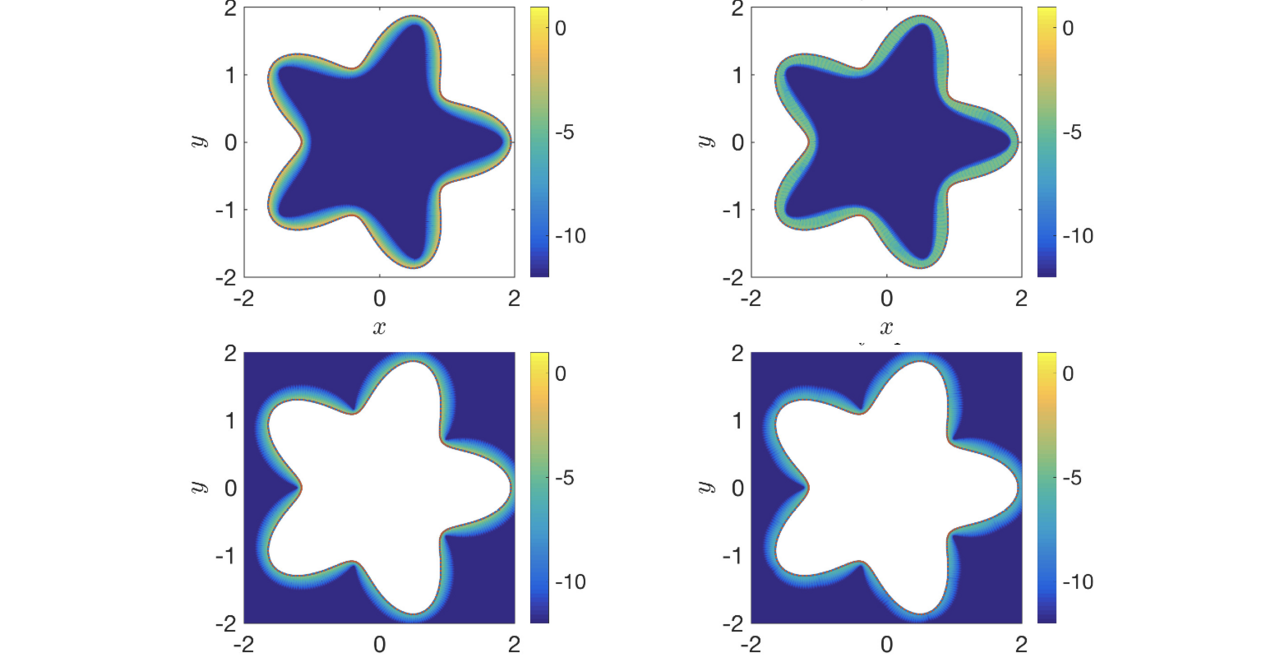
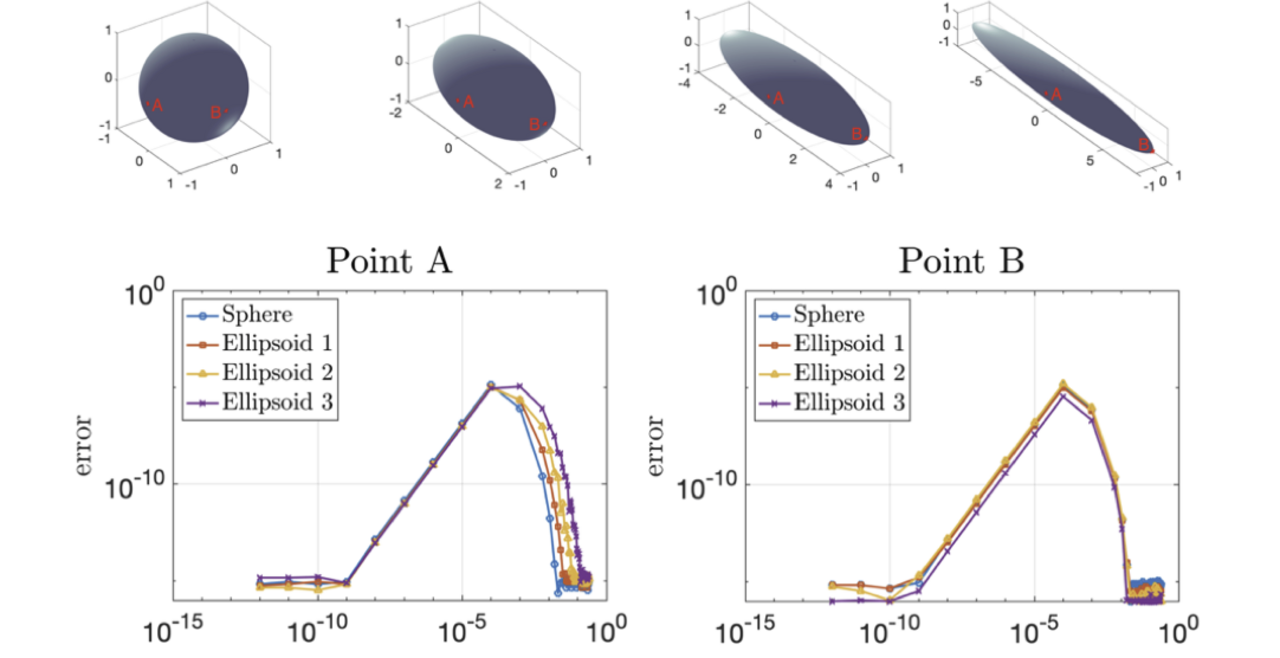
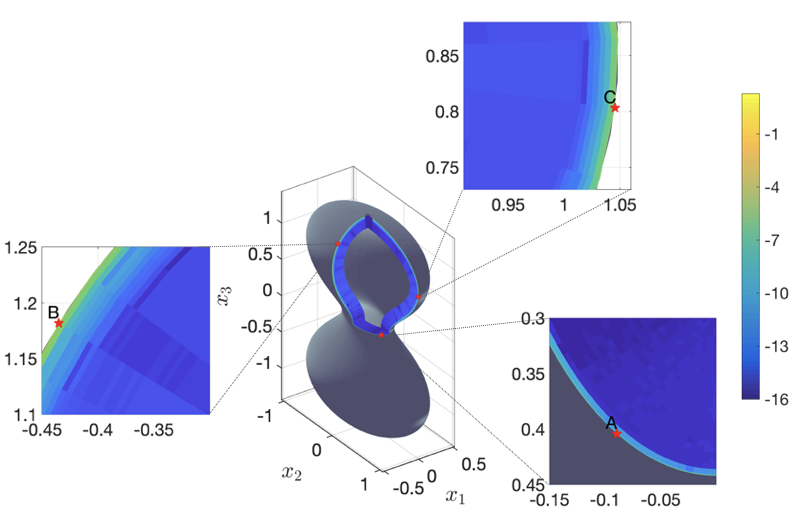
Boundary Integral Methods: The Close Evaluation Problem

Boundary integral methods allow us to computationally solve linear, elliptic partial differential equations in a domain by solving an integral equation on the boundary of that domain, a lower dimensional problem than the original problem. This allows for more efficient computational methods. The close evaluation problem is due to the fact that many of these methods are very inaccurate near the boundary of the domain. We have been focusing on developing new numerical methods for the close evaluation problem for Laplace’s equation, the canonical elliptic partial differential equation, in two and three dimensions. The new methods are developed based on conducting an asymptotic analysis and studying the underlying issues, and are easily implementable, making them very useful for applications.

S. Khatri, A. D. Kim, R. Cortez, C. Carvalho, Close evaluation of layer potentials in three dimensions, 423:109798, 2020 (pdf) (link) C. Carvalho, S. Khatri, A. D. Kim, Asymptotic approximation for the close evaluation of double-layer potentials, SIAM Journal on Scientific Computing, 42:A504-A533, 2020 (pdf) (link) C. Carvalho, S. Khatri, A. D. Kim, Asymptotic analysis for close evaluation of layer potentials, Journal of Computational Physics, 355:327-341, 2018 (pdf) (link) C. Carvalho, S. Khatri, and A. D. Kim, Local analysis of near fields in acoustic scattering, 13th International Conference on Mathematical and Numerical Aspects of Wave Propagation, Minneapolis, MN, 2017 (pdf)

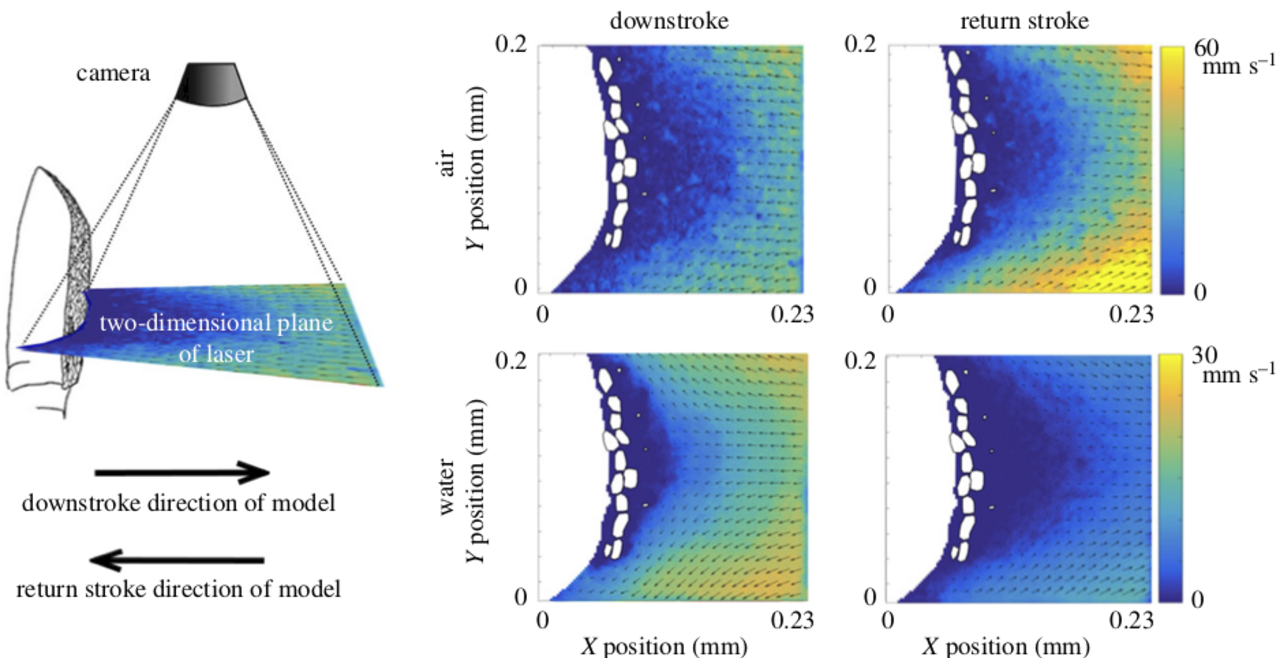
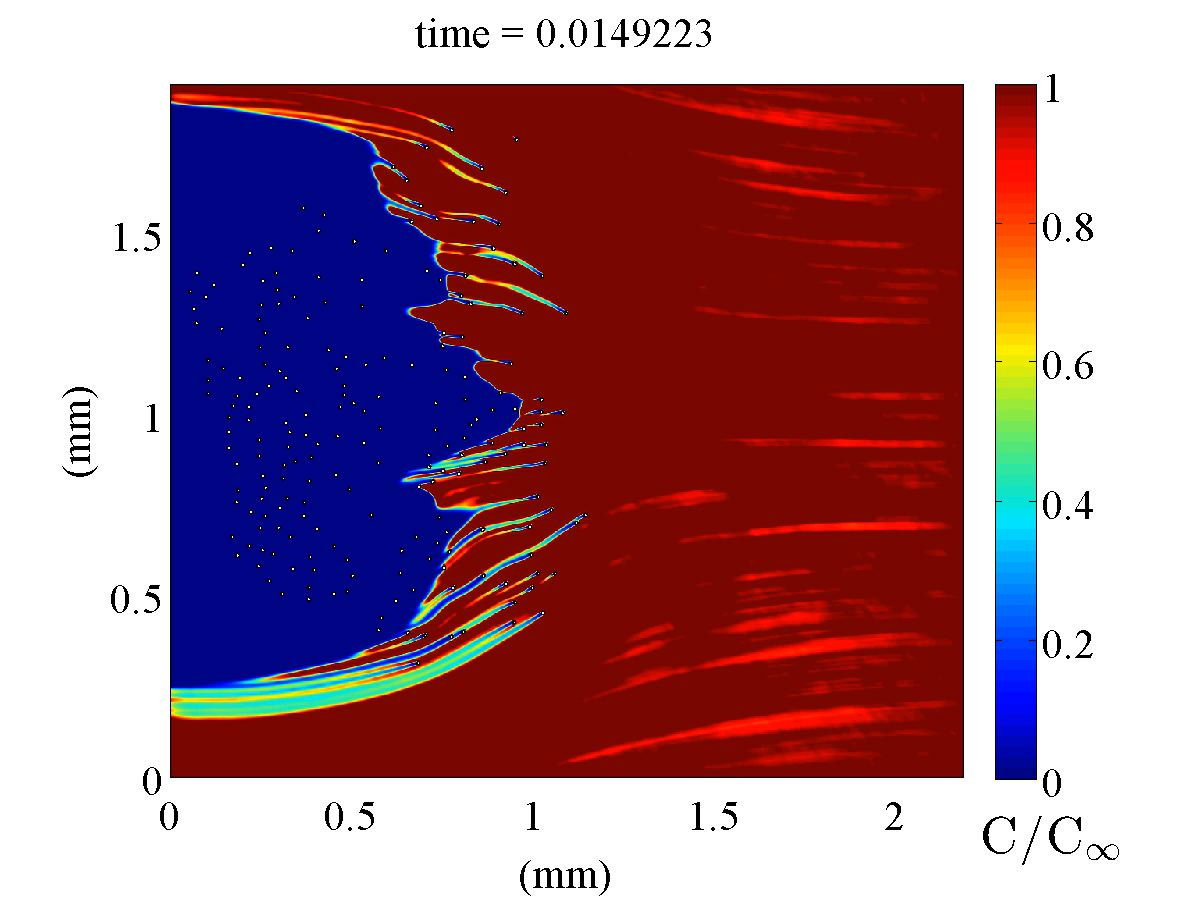
Odorant Molecule Capture by Marine and Terrestial Crabs

The odor-capture organs of crabs, bearing arrays of chemosensory sensilla like fine hairs, rely heavily on the interactions between sensilla and fluid. The morphology differs markedly between marine and terrestrial lineages. It is suspected that the morphology of these organs has evolved differently in order to improve the capturing of odor molecules in the two different fluids. To study the effects of these morphologies, we model the advection and diffusion of concentrations of odor molecules through arrays of sensilla in the flow field, observing how much is captured by the sensilla.

Investigation of Biological Invasions

We are applying the newly developed numerical methods for the surfactant to model biological invasions (Fisher-KPP propagation problems). Biological invasions occur when an invasive species entres a new area. We are studying when there is a road or river on which a species spreads faster (modeled via diffusion and reaction) than in the outlying fields adjacent to the road or river. We are currently investigating transitional states and generalizations of the problem by extending the novel methodology previously developed.

A Numerical Method to Model Surfactants In Multiphase Flow  

We have developed a mathematical model and a two-dimensional numerical method using sharp interface tracking methods to simulate two-phase flow in the presence of surfactants. Surfactants, which modify surface tension, are important in many multiphase flows. Surfactants can help with wetting and foaming and can be used as an emulsifier and dispersant. Applications of these properties include microfluidics, pharmaceuticals, suspensions, and medical applica- tions. The model is novel in that it includes the solubility of the surfactants. The numerical methods useuniform grids for the entire problem, which for this problem is advantageous over alternative methods.

Surface Stress Induced Entrainment in Stratified Fluids