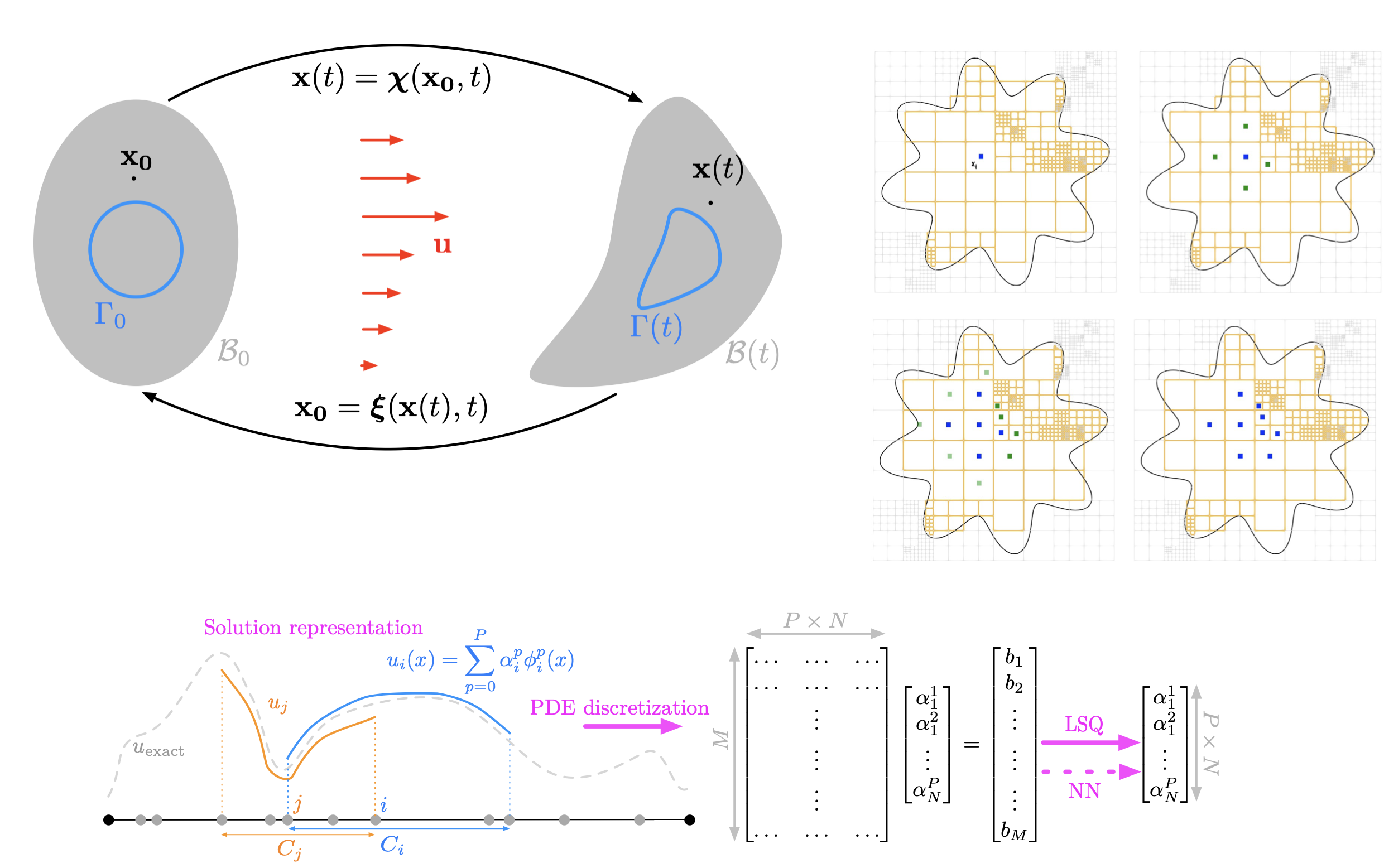
Overview and Philosophy
My research aims to develop mathematical and numerical tools to model, simulate, and investigate a myriad of real-life applications. I strive to complement or replace in vitro experiments with in silico computations to accelerate scientific discovery. Specifically, I design and study computer algorithms capable of solving partial differential equations to simulate continuum representations of problems emanating from Sciences and Engineering. My primary goals are to design algorithms that achieve high accuracy and high performance to produce meaningful results at minimal costs, yet general and flexible enough to be employed in different contexts and thus broaden the collaboration spectrum. I believe that advances in computational sciences help us better understand sciences and engineering and that the constant flow of novel problems drives creativity and innovation in Computational Sciences. Because of this symbiosis, fundamental computational sciences research and simulation of real-life systems are intertwined in my research program. The defining aspects of my research are not the discipline of the applications I study or the applications themselves but rather the underlying mathematical tools I design.
At UC Merced, I have formed the "Mathematical, Applied, and Computational Sciences" (MACS) group, currently composed of myself and 6 Ph.D. students. Our research activities utilize tools and techniques drawn from numerical analysis, machine learning, linear algebra, high-performance computing, mathematical modeling, and scientific visualization. They are articulated along three primary directions
- Direct simulation of incompressible fluid flows
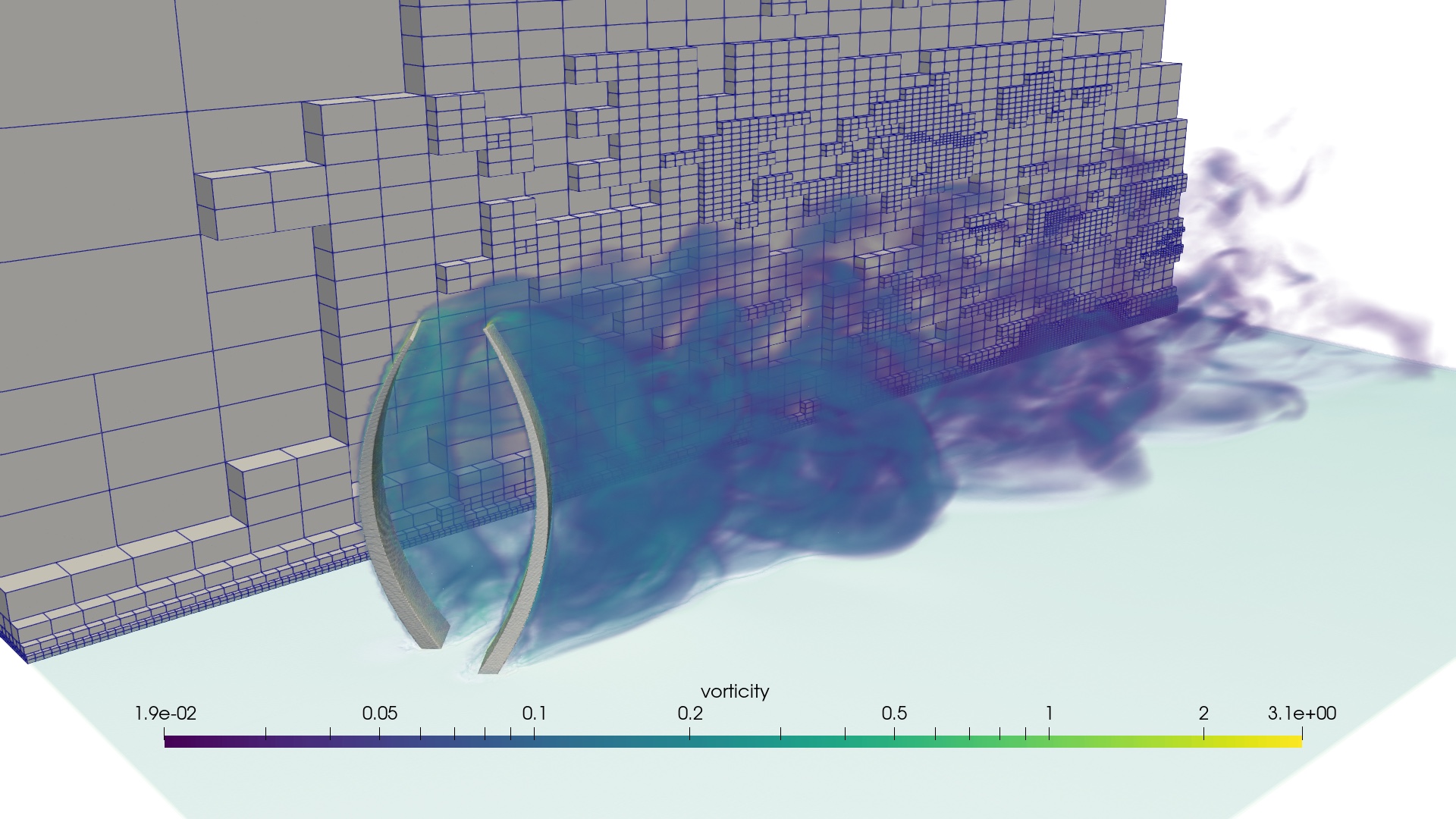
- Computational continuum modeling of biophysical systems

- Numerical methods design assisted by artificial intelligence