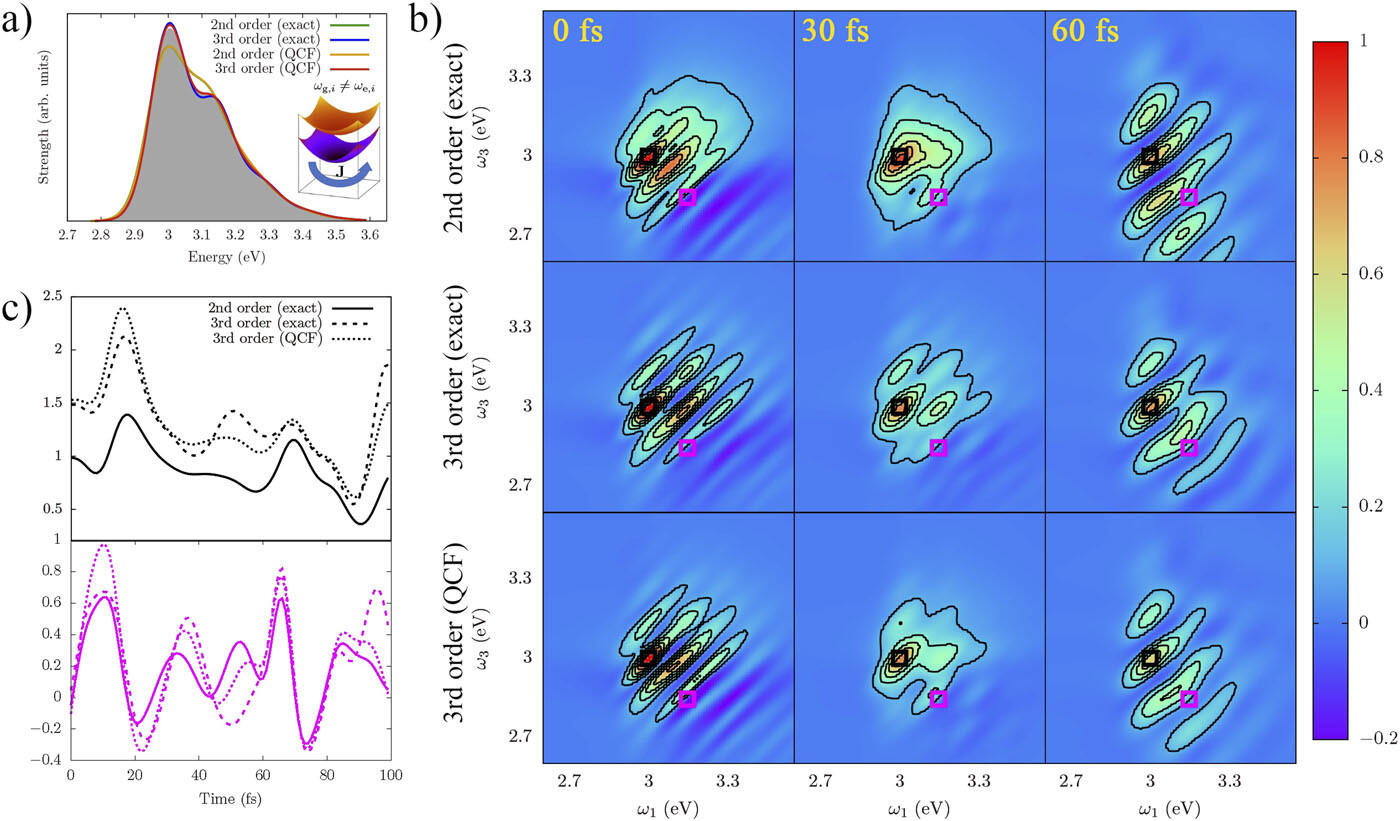
In this manuscript, we develop a novel computational approach for simulating nonlinear optical spectra in the condensed phase. Nonlinear spectroscopy techniques such as 2D electronic spectroscopy (2DES) can directly probe the excited state dynamics of complex systems on a femtosecond timescale, but are often difficult to interpret, making accurate first-principles simulations crucial. Here, we simulate 2DES signals of complex systems based on a cumulant expansion truncated at third order.

Using a simple harmonic model system, we demonstrate that including third order cumulant corrections in the calculation is vital in capturing signatures in the 2DES maps caused by a change in curvature between the ground- and excited state potential energy surfaces, as well as Duschinsky mode mixing. We also show that 2DES signals in the third order cumulant approximation can be accurately constructed based on purely classical correlation functions, opening up the possibility of simulating nonlinear spectra in complex condensed phase environments using correlation functions calculated from molecular dynamics trajectories. To show the strengths of this approach, we simulate 2DES signals for the Methylene blue chromophore in water. We show that the third order cumulant correction is very sensitive to the explicit treatment of the solvent environment in our simulations. Our work thus provides new insight into the complex interplay between solvent polarization effects and couplings of fast chromophore degrees of freedom to electronic excitations in condensed phase systems.